Question

Plz show that


`\tan( (\pi)/(4) - \alpha ) \: \tan( (\pi)/(4) + \alpha ) = 1`
​

Answer 1

The formula for tan(A+B) and tan(A-B) are:

`tan(A+B) = (tan(A)+tan(B))/(1-tan(A)tan(B)) \\\\tan(A-B) = (tan(A)-tan(B))/(1+tan(A)tan(B))`

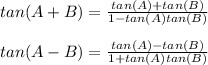
The left hand side of the given expression is:

`tan((\pi)/(4)-\alpha ) tan((\pi)/(4)+\alpha )`

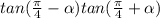
Using the formula above and value of tan(π/4) = 1, we can expand this expression as:

`tan((\pi)/(4)-\alpha ) tan((\pi)/(4)+\alpha )\\\\ = (tan((\pi)/(4) )-tan(\alpha))/(1+tan((\pi)/(4) )tan(\alpha)) * (tan((\pi)/(4) )+tan(\alpha))/(1-tan((\pi)/(4) )tan(\alpha))\\\\ = (1-tan(\alpha))/(1+tan(\alpha)) * (1+tan(\alpha))/(1-tan(\alpha))\\\\ = 1 \\\\ = R.H.S`

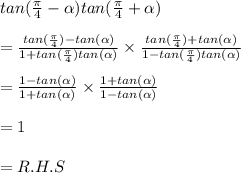
Thus, the left hand side is proved to be equal to right hand side.