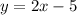Answer: first option.
Explanation:
The equation of the line in Slope-Intercept form is:

Where "m" is the slope of the line and "b" is the y-intercept.
To find "m", we need to substitute the coordinates of the points (4, 3) and (2, -1) into this formula:

We can identify that:
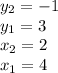
Then:
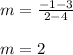
To find "b" we must substitute the slope and one of the given points into
 and solve for "b". Then, this is:
and solve for "b". Then, this is:

Therefore, the equation of this line is: