Answer:
Area = 24 square unit,
Fourth vertex = (-4, -3)
Explanation:
Suppose we have a parallelogram ABCD,
Having vertex A(1, -2), B(2, 3), and C(-3, 2),
Let D(x,y) be the fourth vertex of the parallelogram,
∵ The diagonals of a parallelogram bisect each other,
Thus, the midpoint of AC = midpoint of BD
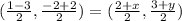
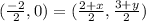
By comparing,
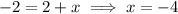
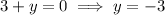
Thus, the fourth vertex is (-4, -3),
Now, the area of the parallelogram ABCD = 2 × area of triangle ABC (Because both diagonals divide the parallelogram in two equal triangles)
Area of a triangle having vertex
 ,
,
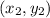 and
and
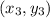 is,
is,
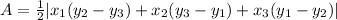
So, the area of triangle ABC
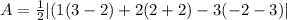
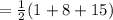
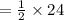
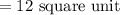
Hence, the area of the parallelogram ABCD = 2 × 12 = 24 square unit.