Question

A tangent from point P to a circle of radius 4 cm is 10 cm long. Find:

a the distance of P from the centre of the circle
b the size of the angle between the tangent and the line joining P to the centre of the
circle.

Answer 1

see explanation

Explanation:

a

The tangent and the radius at the point of contact form a right angle

Using Pythagoras' identity on the right triangle formed.

Let x be the distance from the centre to P, then

x² = 4² + 10² = 16 + 100 = 116 ( take the square root of both sides )

x =
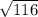`√(116)` ≈ 10.77 cm (to 2 dec. places )

b

let the required angle be Θ, then

Using the sine or cosine ratio in the right triangle.

cosΘ =
`(adjacent)/(hypotenuse)` =
`(10)/(√(116) )`

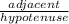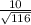
Θ =
`cos^(-1)` (
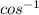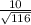`(10)/(√(116) )` ) ≈ 21.8°