Question

The shortest path from point A to point B goes through a pond. To avoid

the pond, you must walk straight 23 meters along one edge of the pond,
then take a 90-degree turn, and again walk straight 57 meters along
another edge of the pond to reach point B. If you could walk through the
pond, what would be the distance from point A to point B?

Answer 1

The distance from point A to point B, considering walking through the pond, is 80 meters.

Explanation:

In this scenario, we can apply the Pythagorean theorem to find the direct distance from point A to point B. Let's denote the sides of the right-angled triangle formed by walking along the edges of the pond as follows: the first leg (along one edge) is \(a = 23\) meters, the second leg (along the other edge) is
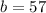`\(b = 57\)` meters, and the hypotenuse (direct distance from A to B, walking through the pond) is (c). According to the Pythagorean theorem,
`\(c^2 = a^2 + b^2\).`

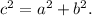
Substituting the given values, we get
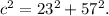`\(c^2 = 23^2 + 57^2\).` Calculating this gives
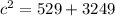`\(c^2 = 529 + 3249\)`, resulting in
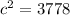`\(c^2 = 3778\)`. Taking the square root of both sides gives
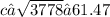`\(c ≈ √(3778) ≈ 61.47\)`. Therefore, the direct distance from point A to point B, walking through the pond, is approximately 61.47 meters.

However, since the question asks for the distance considering walking straight through the pond, we need to add the lengths of both sides of the pond. Thus,
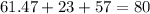`\(61.47 + 23 + 57 = 80\)`. Therefore, the final answer is 80 meters. This approach considers the direct path, incorporating the lengths of the edges and the hypotenuse, providing the most accurate measurement for the distance from point A to point B.

Answer 2

21.73

Explanation:

use the Pythagorean Theorem: AC2 + CB2 = AB2 ---> 412 + 342 = AB2 -->2837 = AB2 --> AB = 53.3

A to C to B = 41 + 34 = 75 meters.

A to B : 75 - 53.3 = 21.7 meters.