Answer:
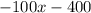
Explanation:
The derivative of a sum is the sum of the derivatives by the sum rule, and this also extends to differences by the constant multiple rule
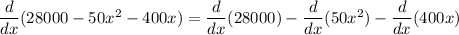
By the constant multiple rule, we have
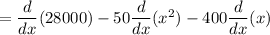
The derivative of any constant is 0.
The power rule says that for any real number
 ,
,
 . And note that
. And note that
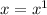 . Thus we have
. Thus we have
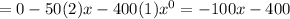
since
