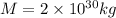Answer:
Part a)
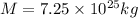
Part b)
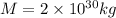
Step-by-step explanation:
Part a)
As we know that the diameter of the planet is given as
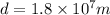
now the radius of the planet is given as
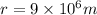
now we know that the acceleration due to gravity of the planet is given by the equation

here we know that
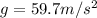
now from above equation we have
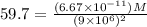
now we have
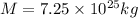
Part b)
Now by kepler's law we know that
time period of revolution of planet about the star is given as
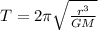
so we have
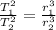
now we have

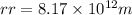
mula of time period
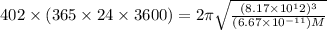
Now we have