Question

The Centers for Disease Control reported the percentage of people 18 years of age and older who smoke (CDC website, December 14, 2014). Suppose that a study designed to collect new data on smokers and nonsmokers uses a preliminary estimate of the proportion who smoke of .31. a. How large a sample should be taken to estimate the proportion of smokers in the population with a margin of error of .02 (to the nearest whole number)? Use 95% confidence.

Answer 1

Answer: 2056

Explanation:

The formula for margin of error for population proportion :-

`E=z_(\alpha/2)*\sqrt{(p(1-p))/(n)}`

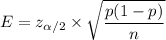
Given : Significance level :
`\alpha = 1-0.95=0.05`

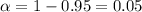
Critical value :
`z_(0.025)=1.96`

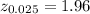
The proportion of people smoke : p=0.31.

Margin of error : E= 0.02

Substitute all the value in the above formula, we get

`0.02=1.96*\sqrt{(0.31(0.69))/(n)}\\\\\Rightarrow\0.0102=\sqrt{(0.2139)/(n)}`

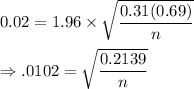
Squaring both sides , we get

`0.00010404=(0.2139)/(n)\\\\\Rightarrow\ n=(0.2139)/(0.00010404)=2055.9400230\approx2056`

Hence, the required sample size = 2056