Answer: 0.33
Explanation:
Let,
- E1 be the coin which has heads in both faces
- E2 be the coin which has tails in both faces
- E3 be the coin which has a head in one face and a tail in the other.
In this question we are using the Bayes' theorem,
where,
P(E1) = P(E2) = P(E3) =

As there is an equal probability assign for choosing a coin.
Given that,
it comes up heads
so, let A be the event that heads occurs
then,
P(A/E1) = 1
P(A/E2) = 0
P(A/E3) =

Now, we have to calculate the probability that the opposite side of coin is tails.
that is,
P(E3/A) = ?
∴ P(E3/A) =
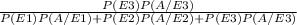
=
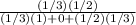
=
 ×
×
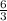
=

= 0.3333 ⇒ probability that the opposite face is tails.