Question

Two long, parallel wires carry unequal currents in the same direction. The ratio of the currents is 3 to 1. The magnitude of the magnetic field at a point in the plane of the wires and 10 cm from each wire is 4.0 μT. What is the larger of the two currents?

Answer 1

3A is the larger of the two currents.

Step-by-step explanation:

Let the currents in the two wires be I₁ and I₂

given:

Magnitude of the electric field, B = 4.0μT = 4.0×10⁻⁶T

Distance, R = 10cm = 0.1m

Ratio of the current = I₁ : I₂ = 3 : 1

Now, the magnitude of a magnetic field at a distance 'R' due to the current 'I' is given as

`B = (\mu_oI)/(2\pi R)`

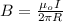
Where
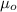`\mu_o` is the magnitude constant = 4π×10⁻⁷ H/m

Thus, the magnitude of a magnetic field due to I₁ will be

`B_1 = (\mu_oI_1)/(2\pi R)`

`B_2 = (\mu_oI_2)/(2\pi R)`

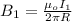
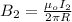
given,

B = B₁ - B₂ (since both the currents are in the same direction and parallel)

substituting the values of B, B₁ and B₂

we get

4.0×10⁻⁶T =
`(\mu_oI_1)/(2\pi R)` -
`(\mu_oI_2)/(2\pi R)`

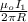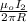
or

4.0×10⁻⁶T =
`(\mu_o)/(2\pi R)* (I_1-I_2 )`

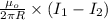
also

`(I_1)/(I_2) = (3)/(1)`

⇒
`I_1 = 3* I_2`

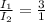
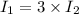
substituting the values in the above equation we get

4.0×10⁻⁶T =
`(4\pi* 10^(-7))/(2\pi 0.1)* (3 I_2-I_2)`

⇒
`I_2 = 1A`

also

`I_1 = 3* I_2`

⇒
`I_1 = 3* 1A`

⇒
`I_1 = 3A`

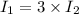
Hence, the larger of the two currents is 3A