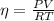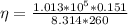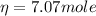Answer:
gas is dioatomic
T_f = 330.0 K
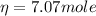
Step-by-step explanation:
Part 1
below equation is used to determine the type Gas by determining
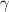 value
value
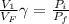
where V_i and V_f is initial and final volume respectively
and P_i and P_f are initial and final pressure
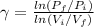
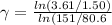
\gamma = 1.38
therefore gas is dioatomic
Part 2
final temperature in adiabatic process is given as
](https://img.qammunity.org/2020/formulas/physics/college/qvnm089594kkzxjoo4gev7q42qu36cjnft.png)
substituing value to get final temperature
![T_f = 260*[(151)/(80.6)]^ {(1.38-1)}](https://img.qammunity.org/2020/formulas/physics/college/jmh9bsjub2n8f1y4tm9ojhnubfaq8lk71h.png)
T_f = 330.0 K
Part 3
determine number of moles by using following formula