Question

Complete the synthetic division problem below.

Answer 1

B

Explanation:

This was originally a third degree polynomial:

`2x^3+4x^2-4x+6`, to be exact.

When you divide by -3, you are basically trying to determine if x + 3 is a zero of that third degree polynomial. The quotient is always one degree lesser than the polynomial you started with, and if there is no remainder, then x + 3 is a zero of the polynomial and you could go on to factor the second degree polynoial completely to get all 3 solutions. To perform the synthetic division, you always first bring down the number in the first position, in our case a 2. Then multiply that 2 by -3 to get -6.

-3| 2 4 -4 6

-6

2 -2

So far this is what we have done. Now we multiply the -3 by the -2 and put that up under the -4 and add:

-3| 2 4 -4 6

-6 6

2 -2 2

Now we multiply the -3 by the 2 to get -6 and put that up under the 6 and add:

-3| 2 4 -4 6

-6 6 -6

2 -2 2 0

That last row gives us the depressed polynomial, which as stated earlier here, is one degree less than what you started with:

`2x^2-2x+2`

Answer 2

Answer: OPTION B

Explanation:

You need to follow these steps:

- Carry the number 2 down and multiply it by the the number -3.

- Place the product obtained above the horizontal line, below the number 4 and add them.

- Put the sum below the horizontal line.

- Multiply this sum by the number -3.

- Place the product obtained above the horizontal line, below the number -4 and add them.

- Put the sum below the horizontal line.

- Multiply this sum by the number -3.

- Place the product obtained above the horizontal line, below the number 6 and add them.

Then:

`-3\ |\ 2\ \ \ \ \ 4\ \ -4\ \ \ \ \ \ 6\\\.\ \ \ \ \ |\ \ \ \ -6\ \ \ \ \ 6\ \ \ -6`

`-----------------`

`.\ \ \ \ \ \ 2\ \ \ -2\ \ \ \ 2\ \ \ \ \ 0`

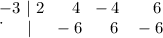
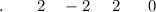
Therefore, the quotient in polynomial form is:

`2x^2-2x+2`