Question

Water flows in a pipe of diameter 450 mm at an average velocity of 3 m/s. Determine the volumetric flow rate and the mass flow rate. How long will it take to fill a tank with measurements 5 m x 6 m x 20 m?

Answer 1

Volumetric flow rate = 0.4773 m³/s

Mass flow rate = 477.3 kg/s

It will take 286.38 seconds to fill a tank with measurements 5 m x 6 m x 20 m

Step-by-step explanation:

Given:

Diameter of the pipe through which the water is flowing = 450 mm

Radius = Diameter/2

Thus, Radius of the pipe = 225 mm

The conversion of mm into m is shown below:

1 mm = 10⁻³ m

Radius of the pipe = 225×10⁻³ m

The area of the cross-section = π×r²

So, Area of the pipe = π×/(225×10⁻³)² m² = 0.1591 m²

Also, Given : The water flowing rate = 3 m/s

Volumetric flow rate is defined as the amount of flow of the fluid in 1 sec.

`Volumetric\ flow= \frac {Volume\ passed}{Time taken}`

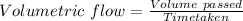
This, can be written as Velocity of the fluid from the cross-section area of the pipe.

Q = A×v

Where,

Q is Volumetric flow rate

A is are though which the fluid is flowing

v is the velocity of the fluid

So,

Q = 0.1591 m²×3 m/s = 0.4773 m³/s

Mass flow rate is defined as the mass of the fluid passes per unit time.

`\dot {m}= \frac {Mass\ passed}{Time taken}`

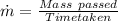
The formula in terms of density can be written as:

`Density=(Mass)/(Volume)`

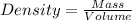
So, Mass:

`Mass= Density * {Volume}`

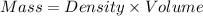
Dividing both side by time, we get:

`\dot {m}= Density * {Q}`

Where,

`\dot {m}` is the mass flow rate

Q is Volumetric flow rate

Density of water = 1000 kg/m³

Thus, Mass flow rate:

`\dot {m}= 1000 * {0.4773} Kgs^(-1)`

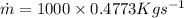
Mass flow rate = 477.3 kg/s

The time taken to fill the volume of measurement 5 m× 6 m× 20 m can be calculated from the formula of volumetric flow rate as:

t= Q×V

So,

Volume of Cuboid = 600 m³

Time = 0.4773 m³/s × 600 m³ = 286.38 s