Question

Water flows in a pipe of diameter 0.5 m. The dianeter of the to 1,0 m. A U-tube manometer is of the enlargement with joining ercury levels 5 mm. Determine the flow rate as well as the pressure 3 Water pipe suddenly enlarges connected to either side pipes which contain water. The difference in m head loss as a result of the enlargement.

Answer 1

Q = 0.943
`m^(3)/s`

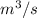
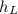`h_(L)` = 0.6605 m

Step-by-step explanation:

Given :

Diameter, d₁ = 0.5 m

Area, A₁ =
`(\pi )/(4)* 0.5^(2)`

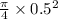
= 0.19625
`m^(2)`

Enlargement diameter, d₂ = 1 m

Enlargement Area, A₂ =
`(\pi )/(4)* 1^(2)`

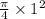
= 0.785
`m^(2)`

Manometric difference, h = 35 mm

=35 X
`10^(-3)` m

From manometer , we get

`P_(1)+\rho _(w).g.z_(1)+\rho _(m).g.h=P_(2)+\rho _(w).g.(z_(1)+h)`

`P_(1)-P_(2)=(\rho _(w)-\rho _(m)).g.h`

`(P_(1)-P_(2))/(\rho _(w).g)=(1-(\rho _(m))/(\rho _(w)))* h`

=
`(1-13.6)* 35* 10^(-3)`

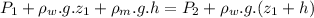
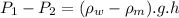
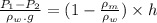
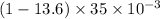
= -0.441

Now from newtons first law,

`(P_(1)-P_(2))/(\rho _(w).g)=(V_(2)^(2)-V_(1)V_(2))/(g)`

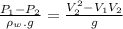
-0.441 =
`(Q^(2))/(9.81)* ((1)/(A_(2)^(2))-(1)/(A_(1)A_(2)))`

-0.441 =
`(Q^(2))/(9.81)* ((1)/(0.785^(2))-(1)/((0.19625* 0.785)^(2)))`

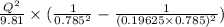
Therefore. Q = 0.943
`m^(3) /s`

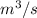
Now V₁ =
`(Q)/(A_(1))`

=
`(0.943)/(0.19625)`

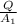
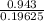
= 4.80 m/s

V₂ =
`(Q)/(A_(2))`

=
`(0.943)/(0.785)`

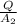
= 1.20 m/s

Therefore, heat loss due to sudden enlargement is given by

`h_(L)=((V_(1)-V_(2))^(2))/(2g)`

`h_(L)=((4.80-1.20)^(2))/(2* 9.81)`

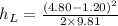
= 0.6605 m