Question

The most popular mathematician in the world is throwing aparty for all of his friends. As a way to kick things off, they decidethat everyone should shake hands. Assuming all 10 people atthe party each shake hands with every other person (but notthemselves, obviously) exactly once, how many handshakes takeplace?

Answer 1

The no. of possible handshakes takes place are 45.

Explanation:

Given : There are 10 people in the party .

To Find: Assuming all 10 people at the party each shake hands with every other person (but not themselves, obviously) exactly once, how many handshakes take place?

Solution:

We are given that there are 10 people in the party

No. of people involved in one handshake = 2

To find the no. of possible handshakes between 10 people we will use combination over here

Formula :
`^nC_r=(n!)/(r!(n-r)!)`

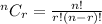
n = 10

r= 2

Substitute the values in the formula

`^(10)C_(2)=(10!)/(2!(10-2)!)`

`^(10)C_(2)=(10!)/(2!(8)!)`

`^(10)C_(2)=(10 * 9 * 8!)/(2!(8)!)`

`^(10)C_(2)=(10 * 9 )/(2 * 1)`

`^(10)C_(2)=45`

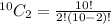
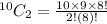
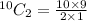
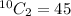
No. of possible handshakes are 45

Hence The no. of possible handshakes takes place are 45.