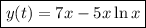a. Substitute the given solutions and their derivatives into the ODE.
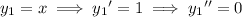
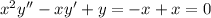
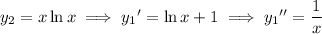
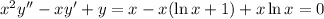
Both solutions satisfy the ODE.
b. The Wronskian determinant is

so the solutions are indeed independent.
c. The ODE has general solution
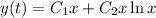 . Then with the given initial conditions, the constants satisfy
. Then with the given initial conditions, the constants satisfy
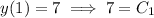
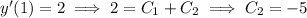
So the ODE has the particular solution,