Answer:
The wavelength of light absorbed in the transition is 459 nm.
Step-by-step explanation:
Energy difference between 5-d and the 6-s sub-levels in gold = ΔE
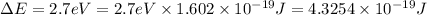
Let the wavelength of light absorbed in the transition 5-d to 6-s be

The relation between energy and wavelength is given by:
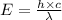
where,
E = energy of photon of the light
h = Planck's constant =

c = speed of light =
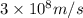
 = wavelength of the photon
= wavelength of the photon

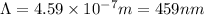
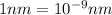
The wavelength of light absorbed in the transition is 459 nm.