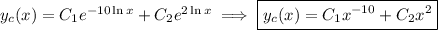Question

Use the substitution of x=e^{t} to transform the given Cauchy-Euler differential equation to a differential equation with constant coefficients then solve that by any method. (finding the characterristic (auxiliary) equation or variation of parameters). Do not forget to re-subtitute for x after you solve the equation.

x^{2}y^{''}+9xy^{'}-20y=0

Answer 1

By the chain rule,

`(\mathrm dy)/(\mathrm dx)=(\mathrm dy)/(\mathrm dt)(\mathrm dt)/(\mathrm dx)\implies(\mathrm dy)/(\mathrm dt)=x(\mathrm dy)/(\mathrm dx)`

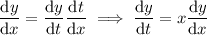
which follows from
`x=e^t\implies t=\ln x\implies(\mathrm dt)/(\mathrm dx)=\frac1x`.

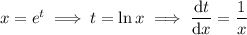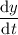`(\mathrm dy)/(\mathrm dt)` is then a function of
`x`; denote this function by
`f(x)`. Then by the product rule,

`(\mathrm d^2y)/(\mathrm dx^2)=(\mathrm d)/(\mathrm dx)\left[\frac1x(\mathrm dy)/(\mathrm dt)\right]=-\frac1{x^2}(\mathrm dy)/(\mathrm dt)+\frac1x(\mathrm df)/(\mathrm dx)`

and by the chain rule,

`(\mathrm df)/(\mathrm dx)=(\mathrm df)/(\mathrm dt)(\mathrm dt)/(\mathrm dx)=\frac1x(\mathrm d^2y)/(\mathrm dt^2)`

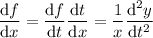
so that

`(\mathrm d^2y)/(\mathrm dt^2)-(\mathrm dy)/(\mathrm dt)=x^2(\mathrm d^2y)/(\mathrm dx^2)`

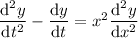
Then the ODE in terms of
`t` is

`(\mathrm d^2y)/(\mathrm dt^2)+8(\mathrm dy)/(\mathrm dt)-20y=0`

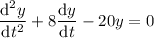
The characteristic equation

`r^2+8r-20=(r+10)(r-2)=0`

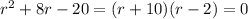
has two roots at
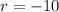`r=-10` and
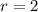`r=2`, so the characteristic solution is

`y_c(t)=C_1e^(-10t)+C_2e^(2t)`

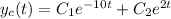
Solving in terms of
`x` gives

`y_c(x)=C_1e^(-10\ln x)+C_2e^(2\ln x)\implies\boxed{y_c(x)=C_1x^(-10)+C_2x^2}`