Given:
Let the speed of sound be represented by 'v' then
v ∝
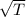 (1)
(1)
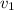 = 349 m/s
= 349 m/s
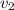 = 340 m/s
= 340 m/s
 = 20°C = 273+20 = 293 K
= 20°C = 273+20 = 293 K
Formulae used:
1) °C = K + 273
2) K = °C - 273
3) °F = 1.8°C + 32
4) °R = °F + 459.67
Solution:
From eqn (1),
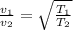
 =
=
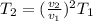
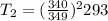 = 278.08 K
= 278.08 K
Now, Usinf formula (1), (2), (3) and (4) respectively, we get
1) T = 293 K
2) T = 293 -278.8 = 5.08°C
3) T = 1.8(5.08) + 32=41.14°F
4) T = 41.14 + 459.67 = 500.81°R