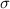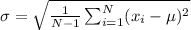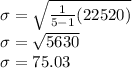Question

A sample of 5 hotels reported the price for a night's stay:

$189 $219 $259 $329 $129
What is the range of the prices of a night’s stay? How to find the standard deviation of the nightly prices

Answer 1

a) Range = 200

b) Standard Deviation = 75.03

Explanation:

Prices: $189 $219 $259 $329 $129

a) Range

Range = Maximum value - Minimum value

Maximum value = 329

Minimum value = 129

So, Range = 329 - 129

Range = 200

b) Standard Deviation

The formula used for finding standard deviation is:

`\sigma=\sqrt{(1)/(N-1)\sum_(i=1)^N(x_(i)-\mu)^2}`

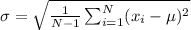
N is No of terms

μ is mean

Mean μ = (189+219+259+329+129)/5 = 225

x x-μ (x-μ)^2

189 189-225= -36 1296

219 219 - 225= -6 36

259 259-225= 34 1156

329 329-225=104 10,816

129 129-225=-96 9216

Now, find
`\sum_(i=1)^N(x_(i)-\mu)^2`

`\sum_(i=1)^N(x_(i)-\mu)^2=1296+36+1156+10816+9216`

`\sum_(i=1)^N(x_(i)-\mu)^2=22520`

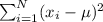
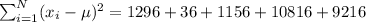
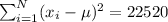
Now finding standard deviation
`\sigma`

`\sigma=\sqrt{(1)/(N-1)\sum_(i=1)^N(x_(i)-\mu)^2}`

`\sigma=\sqrt{(1)/(5-1)(22520)}\\\sigma=√(5630)\\\sigma=75.03`