Question

The activation energy for the uncatalyzed decomposition of hydrogen peroxide at 20°C is 75.3 kJ/mol. In the presence of the enzyme catalase, the activation energy is reduced to 29.3 kJ/mol. Use the following form of the Arrhenius equation, RT ln1k1/k22 5 Ea2 2 Ea1 , to calculate how much larger the rate constant of the catalyzed reaction is.

Answer 1

The rate of enzyme catalyzed reaction will increases by
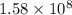`1.58* 10^(8)` times.

Step-by-step explanation:

According to the Arrhenius equation,

`K=A* e^{(-Ea)/(RT)}`

`\log K=\log A-(Ea)/(2.303* RT)`

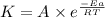
The expression used with catalyst and without catalyst is,

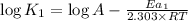`\log K_1=\log A-(Ea_1)/(2.303* RT)`...(1)

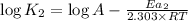`\log K_2=\log A-(Ea_2)/(2.303* RT)`...(2)

On subtracting (2) from (1)

`\log (K_2)/(K_1)=(Ea_1-Ea_2)/(2.303RT)`

where,

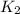`K_2` = rate of reaction with catalyst

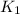`K_1` = rate of reaction without catalyst

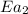`Ea_2` = activation energy with catalyst = 29.3 kJ/mol = 29300 J/mol

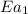`Ea_1` = activation energy without catalyst = 75.3 kJ/mol=75300 J/mol

R = gas constant =8.314 J /mol K

T = temperature =
`20^oC=273+20=293K`

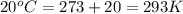
Now on substituting all the values in the above formula, we get

`\log (K_2)/(K_1)=(75300 kJ/mol-29300 kJ/mol)/(2.303* 8.314 J/mol K* 293)=1.58* 10^(8)`

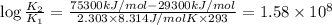
The rate of enzyme catalyzed reaction will increases by
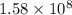`1.58* 10^(8)` times.