Question

Sixty percent of the students at a certain school wear neither a ring nor a necklace. Twenty percent wear a ring and 30 percent wear a necklace. If one of the students is chosen randomly, what is the probability that this student is wearing (a) a ring or a necklace?

Answer 1

0.4

Explanation:

Given

60 % wear neither ring nor a necklace

20 % wear a ring

30 % wear necklace

This question can be Solved by using Venn diagram

If one person is choosen randomly among the given student the probability that this student is wearing a ring or necklace is

`P\left ( wear \ ring\ or \ necklace )+P\left ( neither\ ring\ or\ necklace)=1`

`P\left ( wear \ ring\ or\ necklace )=1-0.6=0.4`

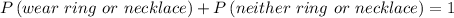
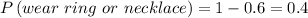
The sum of probabilty is equal to 1 because it completes the set

Therefore the required probabilty is 0.4