Question

Sketch the equilibrium solutions for the following DE and use them to determine the behavior of the solutions.

dy/dt=(y−y^2)

Answer 1

`y=(1)/(1-Ke^(-t))`

Explanation:

Given

The given equation is a differential equation

`(dy)/(dt)=y-y^2`

`(dy)/(dt)=-(y^2-y)`

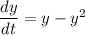
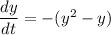
By separating variable

⇒
`(dy)/((y^2-y))=-t`

`\left((1)/(y-1)-(1)/(y)\right)dy=-dt`

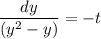
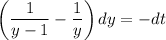
Now by taking integration both side

`\int\left((1)/(y-1)-(1)/(y)\right)dy=-\int dt`

⇒
`\ln (y-1)-\ln y=-t+C`

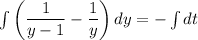
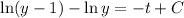
Where C is the constant

`\ln (y-1)/(y)=-t+C`

`(y-1)/(y)=e^(-t+c)`

`(y-1)/(y)=Ke^(-t)`

`y=(1)/(1-Ke^(-t))`

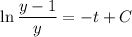
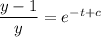
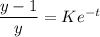
from above equation we can say that

When t will increases in positive direction then
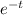`e^(-t)` will decreases it means that
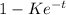`{1-Ke^(-t)}` will increases, so y will decreases. Similarly in the case of negative t.