Question

Suppose a certain population satisfies the logistic equation given by dP

dt = 10P − P
2 with P(0) = 1.
Determine the population when t = 3

Answer 1

The population when t = 3 is 10.

Explanation:

Suppose a certain population satisfies the logistic equation given by

`(dP)/(dt)=10P-P^2`

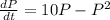
with P(0)=1. We need to find the population when t=3.

Using variable separable method we get

`(dP)/(10P-P^2)=dt`

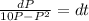
Integrate both sides.

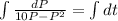`\int (dP)/(10P-P^2)=\int dt` .... (1)

Using partial fraction

`(1)/(P(10-P))=(A)/(P)+(B)/((10-P))`

`A=(1)/(10),B=(1)/(10)`

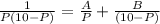
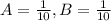
Using these values the equation (1) can be written as

`\int ((1)/(10P)+(1)/(10(10-P)))dP=\int dt`

`\int (dP)/(10P)+\int (dP)/(10(10-P))=\int dt`

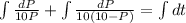
On simplification we get

`(1)/(10)\ln P-(1)/(10)\ln (10-P)=t+C`

`(1)/(10)(\ln (P)/(10-P))=t+C`

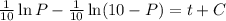
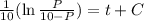
We have P(0)=1

Substitute t=0 and P=1 in above equation.

`(1)/(10)(\ln (1)/(10-1))=0+C`

`(1)/(10)(\ln (1)/(9))=C`

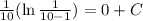
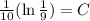
The required equation is

`(1)/(10)(\ln (P)/(10-P))=t+(1)/(10)(\ln (1)/(9))`

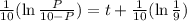
Multiply both sides by 10.

`\ln (P)/(10-P)=10t+\ln (1)/(9)`

`e^{\ln (P)/(10-P)}=e^{10t+\ln (1)/(9)}`

`(P)/(10-P)=(1)/(9)e^(10t)`

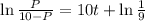
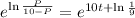
Reciprocal it

`(10-P)/(P)=9e^(-10t)`

`P(t)=(10)/(1+9e^(-10t))`

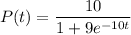
The population when t = 3 is

`P(3)=(10)/(1+9e^(-10\cdot 3))`

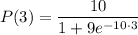
Using calculator,

`P=9.999\approx 10`

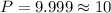
Therefore, the population when t = 3 is 10.