Question

ome metal oxides can be decomposed to the metal and oxygen under reasonable conditions. 2 Ag2O(s) → 4 Ag(s) + O2(g) Thermodynamic data are given below. 2 Ag2O(s) → 4 Ag(s) + O2(g) ΔH°f(kJ/mol) –31.1 -- -- S°(J/K·mol) 121.3 42.55 205.07 What are the values of ΔH°, ΔS° and ΔG°?

Answer 1

Answer : The values of
`\Delta H^o,\Delta S^o\text{ and }\Delta G^o` are
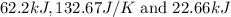`62.2kJ,132.67J/K\text{ and }22.66kJ` respectively.

Explanation :

The given balanced chemical reaction is,

`2Ag_2O(s)\rightarrow 4Ag(s)+O_2(g)`

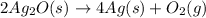
First we have to calculate the enthalpy of reaction
`(\Delta H^o)`.

`\Delta H^o=H_f_(product)-H_f_(product)`

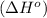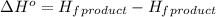
`\Delta H^o=[n_(Ag)* \Delta H_f^0_((Ag))+n_(O_2)* \Delta H_f^0_((O_2))]-[n_(Ag_2O)* \Delta H_f^0_((Ag_2O))]`

where,

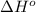`\Delta H^o` = enthalpy of reaction = ?

n = number of moles

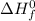`\Delta H_f^0` = standard enthalpy of formation

Now put all the given values in this expression, we get:

`\Delta H^o=[4mole* (0kJ/mol)+1mole* (0kJ/mol)}]-[2mole* (-31.1kJ/mol)]`

`\Delta H^o=62.2kJ=62200J`

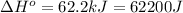
conversion used : (1 kJ = 1000 J)

Now we have to calculate the entropy of reaction
`(\Delta S^o)`.

`\Delta S^o=S_f_(product)-S_f_(product)`

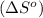`\Delta S^o=[n_(Ag)* \Delta S_f^0_((Ag))+n_(O_2)* \Delta S_f^0_((O_2))]-[n_(Ag_2O)* \Delta S_f^0_((Ag_2O))]`

where,

`\Delta S^o` = entropy of reaction = ?

n = number of moles

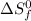`\Delta S_f^0` = standard entropy of formation

Now put all the given values in this expression, we get:

`\Delta S^o=[4mole* (42.55J/K.mole)+1mole* (205.07J/K.mole)}]-[2mole* (121.3J/K.mole)]`

`\Delta S^o=132.67J/K`

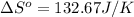
Now we have to calculate the Gibbs free energy of reaction
`(\Delta G^o)`.

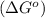As we know that,

`\Delta G^o=\Delta H^o-T\Delta S^o`

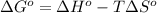
At room temperature, the temperature is 298 K.

`\Delta G^o=(62200J)-(298K* 132.67J/K)`

`\Delta G^o=22664.34J=22.66kJ`

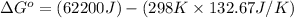
Therefore, the values of
`\Delta H^o,\Delta S^o\text{ and }\Delta G^o` are
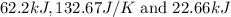`62.2kJ,132.67J/K\text{ and }22.66kJ` respectively.