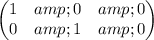Question

Suppose that T : R3 → R2 is given by:

T(a b c) = (a b)
a. Prove that T is a linear transformation.
b. Find the matrix A such that T(x) = Ax.

Answer 1

To prove that T is a linear transformation, we need to show that it satisfies the two properties of linearity: additivity and scalar multiplication. The matrix A such that T(x) = Ax is A = [1 0 0; 0 1 0].

Step-by-step explanation:

A. To prove that T is a linear transformation, we need to show that it satisfies the two properties of linearity: additivity and scalar multiplication.

Additivity: T(u + v) = T(u) + T(v) for all u, v in R3. Let u = (a1, b1, c1) and v = (a2, b2, c2). Then T(u + v) = T((a1 + a2, b1 + b2, c1 + c2)) = (a1 + a2, b1 + b2) = (a1, b1) + (a2, b2) = T(u) + T(v), which shows additivity.

Scalar Multiplication: T(ku) = kT(u) for all u in R3 and k in R. Let u = (a, b, c) and k be a scalar. Then T(ku) = T(ka, kb, kc) = (ka, kb) = k(a, b) = kT(u), which shows scalar multiplication.

B. To find the matrix A such that T(x) = Ax, we can observe that the matrix A will have the same entries as the transformation T. So, A = [1 0 0; 0 1 0].

Answer 2

Answer: The required answers are

(a) T is proved to be a linear transformation.

(b) The matrix A such that T(x) = Ax is
`\begin{pmatrix}1 & 0 &0 \\ 0 & 1 &0 \end{pmatrix}`

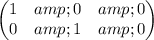
Step-by-step explanation: We are given a linear transformation T : R³ → R² defined as follows :

`T(a,b,c)=(a,b).`

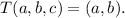
We are to

(a) prove that T is a linear transformation

and

(b) find a matrix A such that T(x) = Ax.

(a) Let s, t are any real numbers and (a, b, c), (a', b', c') ∈ R³.

Then, we have

`T(s(a,b,c)+t(a',b',c'))\\\\=T(sa+ta',sb+tb',sc+tc')\\\\=(sa+ta',sb+tb')\\\\=(sa,sb)+(ta'+tb')\\\\=s(a,b)+t(a',b')\\\\=sT(a,b,c)+tT(a',b',c').`

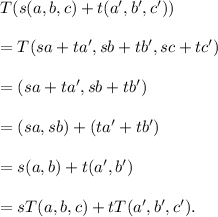
So, we get

`T(s(a,b,c)+t(a',b',c'))=sT(a,b,c)+tT(a',b',c').`

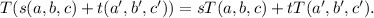
Therefore, T is a linear transformation.

(b) We know that B = {(1, 0, 0), (0, 1, 0), (0, 0, 1)} is a standard basis for R³ and B' = {(1, 0), (0, 1)} is a standard basis for R².

So, we have

`T(1,0,0)=(1,0)=1(1,0)+0(0,1),\\\\T(0,1,0)=(0,1)=0(1,0)+1(0,1),\\\\T(0,0,1)=(0,0)=0(1,0)+0(0,1).`

So, the matrix A such that T(x) = Ax will be given by

`\begin{pmatrix}1 & 0 &0 \\ 0 & 1 &0 \end{pmatrix}`

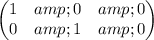
Thus,

(a) T is proved to be a linear transformation.

(b) The matrix A such that T(x) = Ax is
`\begin{pmatrix}1 & 0 &0 \\ 0 & 1 &0 \end{pmatrix}`