Question

Prove that the slope of a constant-volume line is steeper than that for a constant-pressure line for a given state (point) on the T-s diagram.

Answer 1

Step-by-step explanation:

We know that first T-ds equation

Tds=
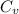`C_v`dT+Pdv

For constant volume process dv=0

⇒Tds=
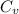`C_v`dT

So
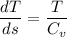`(dT)/(ds)=(T)/(C_v)` ----(1)

We know that second T-ds equation

Tds=
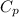`C_p`dT-vdP

For constant pressure process dP=0

⇒Tds=
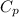`C_p`dT

So
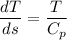`(dT)/(ds)=(T)/(C_p)` ---(2)

We know that
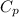`C_p` is always greater than
`C_v`.

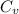So from equation (1) and (2) we can say that slope of constant volume process will be always greater than constant pressure process on T-s diagram.