Question

Mercury flows inside a copper tube 9m long with a 5.1сm inside diameter at an average velocity of 7.0 m/s. The inside surface temperature of the tube is kept at 38 C and the mean temperature of the mercury is 66 C. Assuming that the velocity and temperature profiles are fully developed throughout, calculate the rate of heat transfer by convection. Justify any equations you may use.

Answer 1

rate of heat transfer = 9085708.80 W

Step-by-step explanation:

Given:

Inside diameter, D = 5.1 cm

= 5.1 x
`10^(-2)` m

Average velocity, V = 7 m/s

Mean temperature, T = (66+38) /2

= 52°C

Therefore kinematic viscosity at 52°C is ν = 0.104 X
`10^(-6)`
`m^(2)` / s

Prandtl no., Pr = 0.021

We know Renold No. is

Re =
`(V* D)/(\\u )`

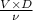
Re =
`(7* 5.1* 10^(-2))/(0.104* 10^(-6))`

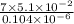
= 3.432 X
`10^(6)`

Therefore the flow is turbulent.

Since the flow is turbulent and the ratio of L/D is greater than 60 we can use Dittua-Boelter equation.

Nu = 0.023
`Re^(0.8)`.
`Pr^(0.3)`

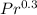
= 0.023 x
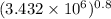`(3.432 *10^(6))^(0.8)` x
`(0.021)^(0.3)`

= 1221.52

Since Nu =
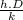
`(h.D)/(k)`

h =
`(k* Nu)/(D)`

=
`(9.4* 1221.52)/(5.1* 10^(-2))`

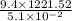
= 225143.3

Therefore rate of heat transfer, q = h.A(T-
`T_(\infty )`

q= 225143.3 x 2πrh ( 66-38)

= 225143.3 X 2π X
`(5.1*10^(-2))/(2)* 9* 28`

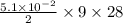
= 9085708.80 W