Question

Matrix question. Please write the detailed formula and explanation/definition of how you did this, thanks.

A=131 232 B= \bigl(\begin{smallmatrix} 211 \\ 323 \\ 211 \end{smallmatrix}\bigr)

a) What is A+B?

b) What is A x B (A times B) ? what is the multiplication formula for 3*3 matrix? How about the multiplication formula for 2*2 matrix and 4*4 matrix?

c) Are A and B invertible? WHY?

Answer 1

a.A+B can not find out

b.
`A* B`=
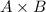`\left[\begin{array}{ccc}13&8&11\\17&10&13\end{array}\right]`

`A* B`=
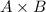`\left[\begin{array}{ccc}a_1b_1+a_2b_4+a_3b_7&a_1b_2+a_2b_5+a_3b_8&a_1b_3+a_2b_6+a_3b_9\\a_4b_1+a_5b_4+a_6b_7&a_4b_2+a_5b_5+a_6b_8&a_4b_3+a_5b_6+a_6b_9\\a_7b_1+a_8b_4+a_9b_7&a_7b_2+a_8b_2+a_8b_5+a_9b_8&a_a_7b-3+a_8b_6+a_9b_9\end{array}\right]`

`A* B`=
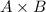`\left[\begin{array}{ccc}a_1b_1+a_2b_3&a_1b_2+a_2b_4\\a_3b_1+a_4b_3&a_3b_2+a_4b_4\end{array}\right]`

In similar way multiply two matrix of order
`4* 4`

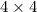
c.No,because A is not a square matrix and determinant of B is zero.

Explanation:

We are given that two matrix

A=
`\left[\begin{array}{ccc}1&3&1\\2&3&2\end{array}\right]`

B=
`\left[\begin{array}{ccc}2&1&1\\3&2&3\\2&1&1\end{array}\right]`

In matrix A , two rows and 3 columns therefore, the order of matrix
`2* 3`

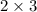
In matrix B, 3 rows and 3 columns therefore, the order of matrix B is
`3* 3`

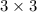
a.A+B can no find because when add two matrix then the order of two matrix should be same .

b.
`A* B`

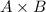
When we multiply on matrix to other matrix then number of columns of first matrix equals to number of rows of second matrix.

Therefore, number of columns of matrix A is equals to number of rows of matrix B.So, we can multiply

`A* B`=
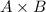`\left[\begin{array}{ccc}1&3&1\\2&3&2\end{array}\right]`\times
`\left[\begin{array}{ccc}2&1&1\\3&2&3\\2&1&1\end{array}\right]`

`A* B`=
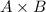`\left[\begin{array}{ccc}13&8&11\\17&10&13\end{array}\right]`

Formula for multiply of matrix of order
`3*3`

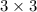
Let A and B are square matrix of order
`3* 3`

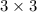
Let A=
`\left[\begin{array}{ccc}a_1&a_2&a_3\\a_4&a_5&a_6\\a_7&a_8&a_9\end{array}\right]` and B=
`\left[\begin{array}{ccc}b_1&b_2&b_3\\b_4&b_5&b_6\\b_7&b_8&b_9\end{array}\right]`

`A* B`=
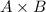`\left[\begin{array}{ccc}a_1b_1+a_2b_4+a_3b_7&a_1b_2+a_2b_5+a_3b_8&a_1b_3+a_2b_6+a_3b_9\\a_4b_1+a_5b_4+a_6b_7&a_4b_2+a_5b_5+a_6b_8&a_4b_3+a_5b_6+a_6b_9\\a_7b_1+a_8b_4+a_9b_7&a_7b_2+a_8b_2+a_8b_5+a_9b_8&a_a_7b-3+a_8b_6+a_9b_9\end{array}\right]`

In similar way we multiply of matrix of order
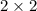`2*2` and matrix multiply of order
`4* 4`

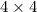
Let A and B are matrix of order
`2* 2`

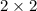
Let
`A=\left[\begin{array}{ccc}a_1&a_2\\a_3&a_4\end{array}\right]`

`B=\left[\begin{array}{ccc}b_1&b_2\\b_3&b_4\end{array}\right]`

`A* B`=
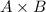`\left[\begin{array}{ccc}a_1b_1+a_2b_3&a_1b_2+a_2b_4\\a_3b_1+a_4b_3&a_3b_2+a_4b_4\end{array}\right]`

In similar way we multiply two matrix of order
`4* 4`

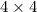
C.Matrix A is not a square matrix .Therefore, it is not a invertible matrix.

`\mid B\mid=\begin{vmatrix}2&1&1\\3&2&3\\2&1&1\end{vmatrix}`

`\mid B\mid=2(2-3)-1(3-6)+1(3-4)=-2+3-1=0`

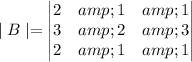
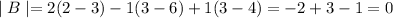
Therefore, the determinant of B is equal to zero therefore, inverse of matrix B does not exist.

Hence, Both matrix A and B are no invertible.