Answer:
The two integers are 18 and 3.
Explanation:
Consider the provided information.
It is given that One integer is 3 more than 5 times another.
Let us consider the integer is x.
Then 3 more than 5 times of x is:
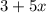
The product of the provided two numbers is 54. i.e.


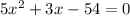
Use the formula of the quadratic equation:
For the equation
 the solutions are:
the solutions are:
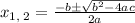
By comparing the obtained equation with the above equation, it can be concluded that a = 5, b = 3 and c = -54. Substitute the these values in the above formula.
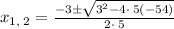
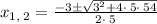
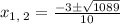
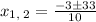
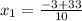 or
or
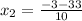
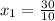 or
or

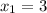 or
or
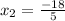
As we have given that numbers are integer, therefore ignore
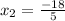
Thus, the value of x is 3 or one number is 3.
Then 3 more than 5 times of x is: 3 + 5(3) = 18.
Therefore, the two integers are 18 and 3.