Question

Which ordered pairs make both inequalities true? Select two options.

y < 5x + 2 y>=1/2x+1

(-1,3)
(0,2)
(1,2)
(2,-1)
(2,2)

Answer 1

c and e

Explanation:

Answer 2

The points C(1,2) and E(2,2) make both inequalities true

Explanation:

we have

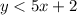`y < 5x+2` -----> inequality A

The solution of the inequality A is the shaded area below the dashed line

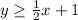`y\geq (1)/(2)x+1` ------> inequality B

The solution of the inequality B is the shaded area above the solid line

The solution of the system of inequalities is the shaded area between the dashed line and the solid line

see the attached figure

Remember that

If a ordered pair is a solution of the system of inequalities, then the ordered pair must satisfy both inequalities and the point lie on the shaded area of the solution

Plot the points and verify if lie on the shaded area

Let

`A(-1,3),B(0,2),C(1,2),D(2,-1),E(2,2)`

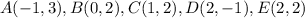
see the attached figure

The points C(1,2) and E(2,2) lie on the shaded area

Note

The points A(-1,3) and B(0,2) satisfy inequality B but don't satisfy inequality A

The point D(2,-1) satisfy inequality A but don't satisfy inequality B

therefore

The points C(1,2) and E(2,2) make both inequalities true