Answer:
Part a)
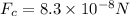
Part b)

Step-by-step explanation:
Part a)
While moving in circular path we know that the acceleration of particle is known as centripetal acceleration
so here we will have
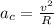
now the net force on the moving electron is given as
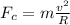
now plug in all values in it

now we have
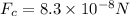
Part b)
Centripetal acceleration is given as
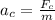
![a_c = \frac{(8.3 * 10^(-8) N){9.1 * 10^(-31)}]()
