Question

Let A elementof M_n(R) be a diagonalizable matrix with tr(A^2) = 0. Prove that A is the zero matrix.

Answer 1

Answer with Step-by-step explanation:

Let A element of
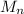`M_n`(R) be a diagonalizable matrix with
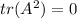`tr(A^2)=0` given

We have to prove that A is the zero matrix

Le A=
`\left[\begin{array} {ccc}a_(11)&0&0\\0&a_(22)&0\\0&0&a_(33)\end{array}\right]` be any matrix of order
`3* 3`

Trace : Trace is defined as the sum of diagonal elements of a matrix.

`A* A=A^2=\left[\begin{array}{ccc}a_(11)&0&0\\0&a_(22)&0\\0&0&a_(33)\end{array}\right]* \left[\begin{array}{ccc}a_(11)&0&0\\0&a_(22)&0\\0&0&a_(33)\end{array}\right]`

`A^2=\left[\begin{array} {ccc}a^2_(11)&0&0\\0&a^2_(22)&0\\0&0&a^2_(33)\end{array}\right]`

Therefore,
`tr(a^2_(11)+a^2_(22)+a^2_(33))=0`

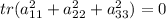
We know that square of an positive or negative element is positive

Therefore, it is necessary that
`a_(11)=0,a_(22)=0,a_(33)=0` when tr(
`A^2)`=0

When all elements of matrix are zero then the matrix should be zero matrix.

Hence, A is a zero matrix .