Answer:
276 feet
Explanation:
The best way to do this is to complete the square, which puts the quadratic in vertex form. The vertex of a negative parabola, which is what this is, is the highest point of the function...the max value. The k coordinate of the vertex will tell us that highest value. To complete the square, we will first set the quadratic equal to 0, then move the constant over to the other side:

The rule for completing the square is that the leading coefficient must be a positive 1. Ours is a negative 16, so we have to factor out -16:
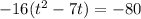
Now the next thing is to take half the linear term, square it, and then add it to both sides. Our linear term is 7, half of that is 7/2. Squaring 7/2 gives you 49/4. So we add 49/9 into the parenthesis on the left. However, we can't forget that there is a -16 out front there that refuses to be ignored. We have to add then (-16)(49/4) onto the right:
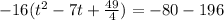
The purpose of this is to create a perfect square binomial that serves as the h value of the vertex (h, k). Stating that perfect square on the left and doing the addition on the right:
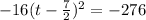
Now we finalize by moving the constant back over and setting it back equal to y:
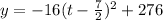
The vertex is
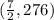
That translates to "at 3.5 seconds the particle is at its max height of 276 feet".