Answer: 0.0018
Explanation:
Binomial distribution formula :-
 , here P(x) is the probability of getting success at x trial , n is the total number of trails, p is the probability of getting success in each trail.
, here P(x) is the probability of getting success at x trial , n is the total number of trails, p is the probability of getting success in each trail.
Given : The probability that a child in the U.S. was living with both parents : p=0.70 ; q=1-0.70=0.30
If 25 children were selected at random in the U.S.,then the probability that at most 10 of them will be living with both of their parents will be :-
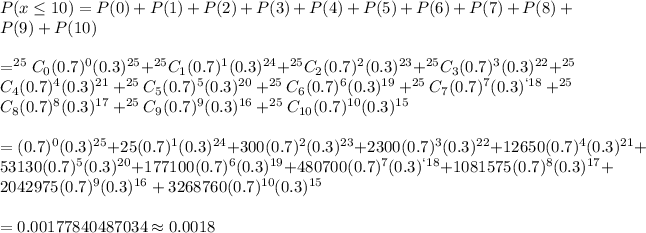
Hence, the probability that at most 10 of them will be living with both of their parents is 0.0018.