Question

If A,B are n×n matrices, then (A + B)^2 = A^2 + 2AB + B^2. Either prove that this statement is true, or explain why it is false.

Answer 1

• The given statement is false.

• The statement is necessarily true when two matrix A and B commute.

Explanation:

This statement is false.

Since, for two matrices A and B , the expansion of the term:

`(A+B)^2` is given by:

`(A+B)^2=(A+B)(A+B)\\\\i.e.\\\\(A+B)^2=A^2+B\cdot A+A\cdot B+B^2`

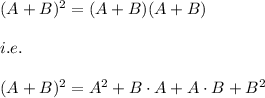
Also, we know that when two matrix A and B commute then we have:

`A\cdot B=B\cdot A`

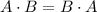
Hence, we get the expression as:

`(A+B)^2=A^2+2A\cdot B+B^2`

But when two matrix A and B do not commute then we need not have:

`(A+B)^2=A^2+2A\cdot B+B^2`