Question

find the value of solid cylinder figure not including cut out: cylinder is 9.7 ft in height, 7 feet in base length, with 4 ft hole cut out.

Answer 1

251.28 cubic feet

Explanation:

The height of the cylinder is 9.7 ft.

The base length is 7 feet. So, the radius(R) =
`(7)/(2) = 3.5 feet`

The length of 4 feet cylinder cut out. So, the radius of the cut cylinder (r) =
`(4)/(2) = 2 feet`

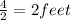
We have to find the volume of solid cylinder figure without cutting part.

= Volume of the whole cylinder - Volume of the hole cut

We know that volume of a cylinder is
`\pi *r^2*h`

Using this formula,

=
`\pi *R^2*h - \pi *r^2*h`

=
`\pi h [R^2 - r^2]`

Here π = 3.14, R = 3.5, r = 2 and h = 9.7

Plug in these values in the above, we get

=
`3.14*9.7 [3.5^2 - 2^2]\\= 30.458[12.25 - 4]\\= 30.458[8.25]\\= 251.2785 ft^3`

When round of to the nearest hundredths place, we get

So, the volume of solid cylinder figure not including cut out= 251.28 cubic feet