Question

How many solutions does the equation x_1 +x_2+x_3+x_4+x_5=21 have where x_1, x_2, x_3, x_4, and x_5 are nonnegative integers and x_1 >= 1?

Answer 1

Explanation:

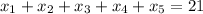`x_(1) + x_(2) + x_(3) + x_(4) + x_(5) = 21\\` (given)

Let us consider :

`x_(1)` =
`t_(1) + 1`

`x_(2)` =
`t_(2)`

`x_(3)` =
`t_(3)`

`x_(4)` =
`t_(4)`

`x_(5)` =
`t_(5)`

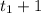
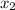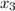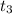
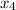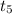
Now, by substituting the above considerations in the above equation, we get:

`t_(1) + 1 + t_(2) + t_(3) + t_(4) + t_(5) = 21\\`

`t_(1)  + t_(2) + t_(3) + t_(4) + t_(5) = 20\\`

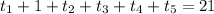
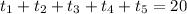
where,

`t_(i)`
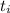
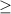`\geq` 1

then it follows

n = 20

r = 4

then no. of solutions for the eqn =
`_(r)^(n + r)\textrm{C}`

=
`_(4)^(24)\textrm{C}`

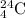
= 10626

Answer :

no. of solutions for the eqn 10626