Question

The angular position of a point on the rim of a rotating wheel is given by θ(t) = 4.0t - 3.0t2 + t3, where θ is in radians and t is in seconds. (a) What is θ(0)? What are the angular velocities at (b) t = 2.0 s and (c) t = 4.0 s? (d) What is the average angular acceleration for the time interval that begins at t = 2.0 s and ends at t = 4.0 s? What are the instantaneous angular accelerations at (e) the beginning and (f) the end of this time interval?

Answer 1

(a) 0 rad

(b) 4 rad/s

(c) 28 rad/s

(d) 12 rad/s^2

(e) 6 rad/s^2

(f) 18 rad/s^2

Step-by-step explanation:

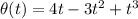`\theta (t)=4t-3t^(2)+t^(3)` .... (1)

(a) here, we need to find angular displacement when t = 0 s

Put t = 0 in equation (1), we get

`\theta (t=0)=0`

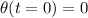
(b) Angular velocity is defined as the rate of change of angular displacement.

ω = dθ / dt

So, differentiate equation (1) with respect to t.

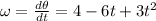`\omega =(d\theta )/(dt)=4-6t+3t^(2)` .... (2)

Angular velocity at t = 2 s

Put t = 2 s in equation (2), we get

ω = 4 - 6 x 2 + 3 x 4 = 4 rad/s

(c) Angular velocity at t = 4 s

Put t = 4 s in equation (2), we get

ω = 4 - 6 x 4 + 3 x 16 = 4 - 24 + 48 = 28 rad/s

(d) Average angular acceleration,

`\alpha =(\omega (t=4s)-\omega (t=2s))/(4-2)`

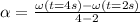
α = (28 - 4) / 2 = 12 rad/s^2

(e) The rate of change of angular velocity is called angular acceleration.

α = dω / dt

α = - 6 + 6 t

At t = 2 s

α = - 6 + 12 = 6 rad/s^2

(f) At t = 4 s

α = - 6 + 24 = 18 rad/s^2