Question

For the equation x^2y" - xy' = 0, find two solutions, show that they are linearly independent and find the general solution. Equations of the form ax^2y" + bxy' + cy = 0 are called Euler's equations or Cauchy-Euler equations. They are solved by trying y = x^r and solving for r (assume that x greaterthanorequalto 0 for simplicity).

Answer 1

The solutions to the differential equation x^2y" - xy' = 0 are y = 1 and y = x, which are linearly independent. The general solution is y = C1 + C2x, where C1 and C2 are constants.

Step-by-step explanation:

For the Cauchy-Euler equation x^2y" - xy' = 0, we find solutions by substituting y = x^r. Differentiating yields y' = rx^{r-1} and y" = r(r-1)x^{r-2}. Substituting these into the equation and simplifying gives us r(r-1)x^r - rx^r = 0, which simplifies to the characteristic equation r^2 - r = 0. Solving this equation, we get the roots r1 = 0 and r2 = 1. Therefore, the two solutions are y1 = x^0 = 1 and y2 = x^1 = x. To show that they are linearly independent, we evaluate the Wronskian determinant W(y1,y2) = |1 x| = x which is nonzero for x > 0. The general solution is a combination of the two: y = C1y1 + C2y2, where C1 and C2 are arbitrary constants.

Answer 2

`y=A+Bx^(2)`

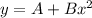
Step-by-step explanation:

The given Cauchy-Euler equation is:
`x^2y''-xy'=0`

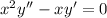
Comparing to the general form:
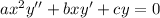`ax^2y''+bxy'+cy=0`, we have a=1,b=-1 and c=0

The auxiliary solution is given by:
`am(m-1)+bm+c=0`

`\implies m(m-1)-m=0`

`\implies m(m-1-1)=0`

`\implies m(m-2)=0`

`\implies m=0\:\:or\:\:m=2`

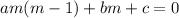
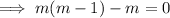
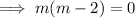
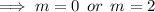
The general solution to this is of the form
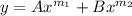`y=Ax^(m_1)+Bx^(m_2)`, where A and B are constants.

`y=Ax^(0)+Bx^(2)`

Therefore the general solution is;

`y=A+Bx^(2)`

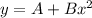
Let
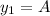`y_1=A` and
`y_2=Bx^2`

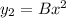
Since we CANNOT express the two solutions as constant multiple of each other, we say the two solutions are linearly independent.

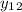`y_1\\eCy_2`, where C is a constant.