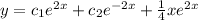Answer:
Solution is
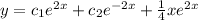
Explanation:
the given equation y''-4y
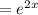 can be written as
can be written as
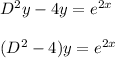
The Complementary function thus becomes
y=c_{1}e^{m_{1}x}+c_{2}e^{m_{2}x}
where
 are the roots of the
are the roots of the
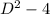
The roots of
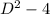 are +2,-2 Thus the comlementary function becomes
are +2,-2 Thus the comlementary function becomes
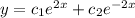
here
 are arbitary constants
are arbitary constants
Now the Particular Integral becomes using standard formula
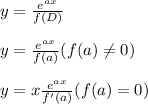
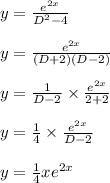
Hence the solution is = Complementary function + Particular Integral
Thus Solution becomes