Question

Divide the polynomial expression:w^2 - w - 3 / w + 1

Answer 1

The division for the provided expression is:
`w-2-(1)/(w+1)`.

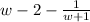Explanation:

Consider the provided polynomial expression:

`(w^2-w-3)/(w+1)`

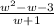
Apply the long division.

Divide the leading coefficients of the numerator
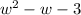`w^2-w-3` and the divisor
`w+1\mathrm{\::\:}(w^2)/(w)=w`

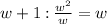
Therefore the quotient is w.

Multiply
`w+1\mathrm{\:by\:}w:\:w^2+w`

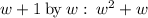
Subtract
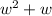`w^2+w` from
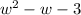`w^2-w-3` to get new remainder.

Thus, the remainder is
`-2w-3`

Therefore,

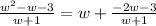`(w^2-w-3)/(w+1)=w+(-2w-3)/(w+1)`......(1)

Divide the leading coefficient of the numerator
`-2w-3` and the divisor
`w+1\mathrm{\::\:}(-2w)/(w)=-2`

Thus the quotient is -2

Now, multiply
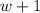`w+1` by -2 which gives
`-2w-2`.

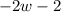Subtract
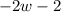`-2w-2` from
`-2w-3` to get new remainder.

Thus, the remainder is -1

Therefore,
`(-2w-3)/(w+1)=-2+(-1)/(w+1)`

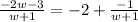
Now replace the value of
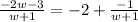`(-2w-3)/(w+1)=-2+(-1)/(w+1)` in equation 1.

Thus, we get
`w-2-(1)/(w+1)`.

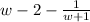Therfore, the division for the provided expression is
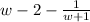`w-2-(1)/(w+1)`.