Question

Enter your answer in the provided box. The usefulness of radiocarbon dating is limited to objects no older than 50,000 yr. What percent of the carbon−14, originally present in a 7.0−g sample, remains after this period of time? The half-life of carbon−14 is 5.73 × 103 yr.

Answer 1

Answer : The percent of the carbon−14 left is, 0.242 %

Explanation :

This is a type of radioactive decay and all radioactive decays follow first order kinetics.

To calculate the rate constant, we use the formula :

`k=(0.693)/(t_(1/2))`

`k=\frac{0.693}{5.73* 10^3\text{ years}}`

`k=1.205* 10^(-4)\text{ years}^(-1)`

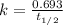
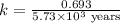
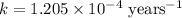
Now we have to calculate the amount left.

Expression for rate law for first order kinetics is given by :

`k=(2.303)/(t)\log(a)/(a-x)`

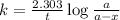
where,

k = rate constant =
`1.205* 10^(-4)\text{ years}^(-1)`

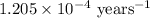
t = time taken for decay process = 50000 years

a = initial amount or moles of the reactant = 7 g

a - x = amount or moles left after decay process = ?

Putting values in above equation, we get:

`1.205* 10^(-4)=\frac{2.303}{50000\text{ years}}\log(7g)/(a-x)`

`a-x=0.0169g`

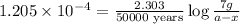
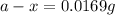
The amount left of carbon-14 = 0.0169 g

Now we have to calculate the percent of the carbon−14 left.

`\text{Percent of carbon}-14\text{ left}=\frac{\text{Amount left of carbon}-14}{\text{Original amount of carbon}-14}* 100`

`\text{Percent of carbon}-14\text{ left}=(0.0169g)/(7g)* 100=0.242\%`

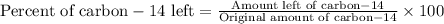
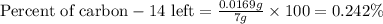
Therefore, the percent of the carbon−14 left is, 0.242 %