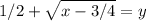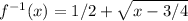Answer:

Explanation:
y=x^2-x+1
We want to solve for x.
I'm going to use completing the square.
Subtract 1 on both sides:
y-1=x^2-x
Add (-1/2)^2 on both sides:
y-1+(-1/2)^2=x^2-x+(-1/2)^2
This allows me to write the right hand side as a square.
y-1+1/4=(x-1/2)^2
y-3/4=(x-1/2)^2
Now remember we are solving for x so now we square root both sides:
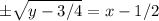
The problem said the domain was 1/2 to infinity and the range was 3/4 to infinity.
This is only the right side of the parabola because of the domain restriction. We want x-1/2 to be positive.
That is we want:
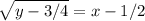
Add 1/2 on both sides:
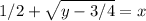
The last step is to switch x and y: