Question

Convert 10.25 degrees into radians; and π, π/2 and π/3 radians into degrees.

Answer 1

10.25° = 0.1790 radians

π radians = 180°

π/2 radians = 90°

π/3 radians = 60°

Step-by-step explanation:

The conversion of degree into radians is shown below:

1° = π/180 radians

So,

10.25° = (π/180)*10.25 radians

Also, π = 22/7

So,

`10.25^0=(22*10.25)/(7*180)radians`

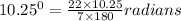
Solving it we get,

10.25° = 0.1790 radians

The conversion of radians into degree is shown below:

1 radian = 180/π°

(a)

π radians = (180/π)*π°

Thus,

π radians = 180°

(b)

π/2 radians = (180/π)*(π/2)°

`\frac {\pi }{2} radians=\frac{180}{\\ot {\pi }} * \frac{\\ot {\pi }}{2}^0`

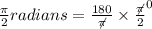
π/2 radians = 90°

(c)

π/3 radians = (180/π)*(π/3)°

`\frac {\pi }{3} radians=\frac{180}{\\ot {\pi }} * \frac{\\ot {\pi }}{3}^0`

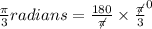
π/3 radians = 60°

Answer 2

0.1788 ,180°,90°,60°

Step-by-step explanation:

CONVERSION FROM DEGREE TO RADIANS: For converting degree to radian we have to multiply with
`(\pi)/(180)`

using this concept 10.25°=10.25×
`(\pi)/(180)`=0.1788

CONVERSION FROM RADIAN TO DEGREE: For converting radian to degree we have to multiply with
`(180)/(\pi)`

using this concept π=π×
`(180)/(\pi)`

=180°

`(\pi)/(2)`=
`(\pi)/(2)[/tex×[tex](180)/(\pi)`

=90°

`(\pi)/(3)`=
`(\pi)/(3)`×
`(180)/(\pi)`

=60°