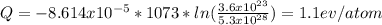Question

Calculate the energy for vacancy formation in silver, given that the equilibrium number of vacancies at 800˚C (1073 K) is 3.6 × 1023 m-3 . The atomic weight and density (at 800˚C) for silver are, respectively, 107.9 g/mol and 9.5 g/cm3 .

Answer 1

The energy for vacancy formation in silver is 1.1 ev/atom

Step-by-step explanation:

The total number of sites is equal to:

`N=(N_(A) \rho )/(A)`

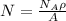
Where

NA = Avogadro´s number = 6.023x10²³atom/mol

A = atomic weight of silver = 107.9 g/mol

ρ = density of silver = 9.5 g/cm³

Replacing:

`N=(6.023x10^(23)*9.5 )/(107.9) =5.3x10^(22) atom/cm^(3) =5.3x10^(28) m^(-3)`

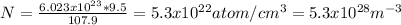
The energy for vacancy is equal:

`Q=-RTln((N_(v) )/(N) )`

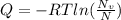
Where

R = 8.314 J/mol K = 8.614x10⁻⁵ev/atom K

T = 800°C = 1073 K

Nv = number of vacancy = 3.6x10²³m⁻³

Replacing:

`Q=-8.614x10^(-5) *1073*ln((3.6x10^(23) )/(5.3x10^(28) ) )=1.1ev/atom`