Question

At a certain university, 50% of all entering freshmen planned to major in a STEM (science, technology, engineering, mathematics) discipline. A sample of 36 freshmen is selected. What is the probability that the proportion of freshmen in the sample is between 0.477 and 0.580?

Answer 1

Answer: 0.4402

Explanation:

Given : The proportion of the registered voters in a country are Republican = P=0.50

Sample space = 36

The test statistic for proportion :-

`z=\frac{p-P}{\sqrt{(P(1-P))/(n)}}`

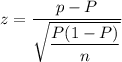
For p= 0.477

`z=\frac{0.477-0.50}{\sqrt{(0.50(1-0.50))/(36)}}\approx-0.276`

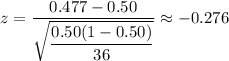
For p= 0.58

`z=\frac{0.58-0.50}{\sqrt{(0.50(1-0.50))/(36)}}\approx0.96`

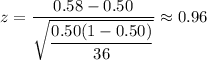
Now, the probability that the proportion of freshmen in the sample is between 0.477 and 0.58 (by using the standard normal distribution table):-

`P(0.477<x<0.58)=P(-0.276<z<0.96)\\\\=P(z<0.96)-P(z<-0.276)\\\\=0.8314724- 0.391274=0.4401984\approx0.4402`

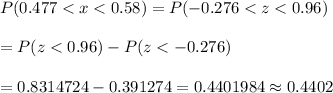
Hence, the probability that the proportion of freshmen in the sample is between 0.477 and 0.580 = 0.4402