Question

An electric motor is to be supported by four identical mounts. Each mount can be treated as a linear prevent problems due required that the amplitude of motion should not exceed 0.1 mm per 1 N of unbalance force. The mass of the motor is 120 kg and the operating speed is 720 rpm Use the concept of transfer function to determine the required stiffhess coefficient of each mount.

Answer 1

GIVEN:

Amplitude, A = 0.1mm

Force, F =1 N

mass of motor, m = 120 kg

operating speed, N = 720 rpm

`(A)/(F)` =
`(0.1* 10^(-3))/(1) = 0.1* 10^(-3)`

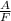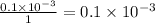
Formula Used:

`A = \frac{F}{\sqrt{(K_(t) - m\omega ^(2)) +(\zeta \omega ^(2))}}`

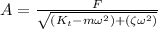
Solution:

Let Stiffness be denoted by 'K' for each mounting, then for 4 mountings it is 4K

We know that:

`\omega = (2 \pi* N)/(60)`

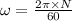
so,

`\omega = (2 \pi* 720)/(60)` = 75.39 rad/s

Using the given formula:

Damping is negligible, so,
`\zeta = 0`

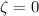
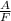`(A)/(F)` will give the tranfer function

Therefore,

`(A)/(F)` =
`\frac{1}{\sqrt{(4K - 120\ ^(2))}}`

`0.1* 10^(-3)` =
`\frac{1}{\sqrt{(4K - 120\ ^(2))}}`

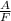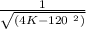
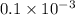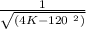
Required stiffness coefficient, K = 173009 N/m = 173.01 N/mm