Question

An ac source is connected to a resistor R = 75Ω, an inductor L = 0.01 H, and a capacitor C = 4 μF. What is the phase difference φ between the voltage of the source and the current in the circuit when the frequency of the source is equal to half the resonance frequency of the circuit?

Answer 1

135°.

Step-by-step explanation:

R = 75 ohm, L = 0.01 H, C = 4 micro F = 4 x 10^-6 F

Frequency is equal to the half of resonant frequency.

Let f0 be the resonant frequency.

`f_(0)=(1)/(2\pi √(LC))`

`f_(0)=\frac{1}{2* 3.14 \sqrt{0.01* 4* 10^(-6)}}`

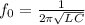
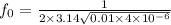
f0 = 796.2 Hz

f = f0 / 2 = 398.1 Hz

So, XL = 2 x 3.14 x f x L = 2 x 3.14 x 398.1 x 0.01 = 25 ohm

`X_(c)=(1)/(2\pi fC)`

Xc = 100 ohm

`tan\phi = \frac{X_(L)-_{X_(C)}}{R}`

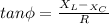
tan Ф = (25 - 100) / 75 = - 1

Ф = 135°

Thus, the phase difference is 135°.