Question

An electron is to be accelerated in a uniform electric field having a strength of 2.00 × 106 V/m. (a) What energy in keV is given to the electron if it is accelerated through 0.400 m? (b) Over what distance would it have to be accelerated to increase its energy by 50.0 GeV?

Answer 1

a) 800 keV

b) 24.996 km.

Step-by-step explanation:

(a) we have

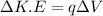`\large \Delta K.E=q\Delta V` .............(1)

where,

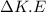`\large \Delta K.E` = Change in kinetic energy

`q` = charge of an electron

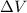`\Delta V` = Potential difference

also

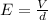`\large E=(V)/(d)` .......(2)

E = electric field

d = distance traveled

Now from (1) and (2) we have,

`\large \Delta K. E=qV=qEd`

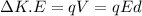
substituting the values in the above equation, we get

`\large \Delta K. E=(1.6* 10^(-19)C)(2* 10^6V/m)(0.400m)((1eV)/(1.6* 10^(-19)J))((1keV)/(1000eV))`

`\large \Delta K. E=800keV`

Thus, the energy gained by the electron is 800 keV if it is accelerated over a distance of 0.400 m.

(b) Using the equation (1), we have

`\large d=(\Delta K.E)/(qE)`

`\large d=((50* 10^9eV))/((1.6* 10^(-19C))(2* 10^6V/m))((1.6* 10^(-19)J)/(1eV))`

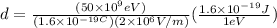
or

`\large d=2.4996* 10^4m`

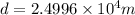
or

`\large d=24.996* 10^3m=24.996km`

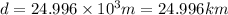
Thus, to gain 50.0 GeV of energy the electron must be accelerated over a distance of 24.996 km.

Answer 2

a) 800 keV

b) 25 km

Step-by-step explanation:

`Strength\ of\ Electric\ field=2* 10^6\ V/m\\a)\ Potential\ Difference=Strength\ of\ Electric\ field* Distance\\\Rightarrow Potential\ Difference=Kinetic\ Energy\ =2* 10^6* 0.4\\\therefore Energy=0.8* 10^6\ eV=800\ keV\\`

`b)\ Potential\ difference=50\ GeV=50* 10^9\ eV\\Distance=(Potential\ difference)/(electric\ field)\\\Rightarrow Distance=(50* 10^9)/(2* 10^6)\\\Rightarrow Distance=25* 10^3\ m\\\therefore Distance=25\ km`